2020年 5月28日
問 1. 事象 \( A \) と \( B \) とが互いに独立で、\( P(A) = 5/7 \) 、\( P(B) = 14/15 \)であるとき、次の確率を求めなさい。
ただし、解答は分数で m/n のように答えなさい。
(1) \( P(A \cap B) \)
(2) \( P( A \cap \overline{B}) \)
(3) \( P( A \cup \overline{B} ) \)
問 2. ある情報機器製造会社では、3つの工場 \( A \)、\( B \)、\( C \) で同じ情報通信機器を製造している。この製品のうち、50%を \( A \) 、30%を \( B \) 、20%を \( C \) で製造しているものとする。また、不良品の割合は、\( A \) が 2%、\( B \) が 5%、\( C \) が 10%であるものとする。このとき、ある製品が不良品だったとき、それが \( B \) で製造された確率を求めなさい。
ただし、解答は分数で m/n のように答えなさい。
問3. ある2元通信路では、2元記号 \( \{ a, b \} \) を用いて通信する。記号 \( a \)、\( b \) に対する受信信号 \( Y_a \)、\( Y_b \) はそれぞれ正規分布 \( N(c, 4) \)、\( N(d, 4) \) に従い、\( \{ s < Y_a \le t \} \)、\( \{ t < Y_b \le u \} \) のときに限り誤りが発生しないという(これらの条件が満たされなければ必ず誤りが生じるものとする)。なお、\( a \)、\( b \) を送信する確率は、それぞれ \( P(a) = 3/5 \)、\( P(b) = 2/5 \) とする。
| \( z \) | \( I(z) \) |
| 0.00 | 0.00000 |
| 0.25 | 0.09871 |
| 0.50 | 0.19146 |
| 0.75 | 0.27337 |
| 1.00 | 0.34134 |
| 1.25 | 0.39435 |
| 1.50 | 0.43319 |
| 1.75 | 0.45994 |
| 2.00 | 0.47725 |
| 2.25 | 0.48778 |
| 2.50 | 0.49379 |
| 2.75 | 0.49702 |
| 3.00 | 0.49865 |
| 3.25 | 0.49942 |
| 3.50 | 0.49977 |
| 3.75 | 0.49991 |
| 4.00 | 0.49997 |
このとき、上に示す標準正規分布表を用いて次の確率を求めなさい。
ただし、\(c\)、\(d\)、\(s\)、\(t\)、\(u\) は学籍番号の下1桁により、以下の値を用いて計算しなさい(小数で解答しなさい)。
学籍番号下1桁 0 \(c=3.00\)、\(d=7.00\)、\(s=0.50\)、\(t=4.00\)、\(u=8.50\)
学籍番号下1桁 1 \(c=3.50\)、\(d=7.50\)、\(s=0.50\)、\(t=4.00\)、\(u=8.50\)
学籍番号下1桁 2 \(c=3.00\)、\(d=7.00\)、\(s=1.00\)、\(t=4.50\)、\(u=9.00\)
学籍番号下1桁 3 \(c=3.50\)、\(d=7.50\)、\(s=1.00\)、\(t=4.50\)、\(u=9.00\)
学籍番号下1桁 4 \(c=3.00\)、\(d=7.00\)、\(s=1.50\)、\(t=5.00\)、\(u=9.50\)
学籍番号下1桁 5 \(c=3.50\)、\(d=7.50\)、\(s=1.50\)、\(t=5.00\)、\(u=9.50\)
学籍番号下1桁 6 \(c=3.00\)、\(d=7.00\)、\(s=2.00\)、\(t=5.50\)、\(u=10.00\)
学籍番号下1桁 7 \(c=3.50\)、\(d=7.50\)、\(s=2.00\)、\(t=5.50\)、\(u=10.00\)
学籍番号下1桁 8 \(c=3.00\)、\(d=7.00\)、\(s=2.50\)、\(t=6.00\)、\(u=10.50\)
学籍番号下1桁 9 \(c=3.50\)、\(d=7.50\)、\(s=2.50\)、\(t=6.00\)、\(u=10.50\)
(1) 記号 \( a \) に対する誤り率 \(P(誤|a)\)
(2) 記号 \( b \) に対する誤り率 \( P(誤|b) \)
(3) この通信路の誤り率 \( P(誤) \)(小数点以下3桁で解答しなさい)
問4. ある2元対称消失通信路の送信記号 \(X\) を
\( X = \left\{ \begin{array}{cc} x_1 , & x_2 \\ 2/3 , & 1/3 \end{array} \right\} \) (\(x_1, x_2\) の生起確率 \(P(x_1)=2/3 , P(x_2)=1/3\))
受信記号 \(Y\) を
\( Y = \left\{ \begin{array}{ccc} y_1 , & y_2 , & y_3 \end{array} \right\} \)
通信路行列 \(P\) を
\( P = \left[ \begin{array}{ccc} P(y_1|x_1) & P(y_2|x_1) & P(y_3|x_1) \\ P(y_1|x_2) & P(y_2|x_2) & P(y_3|x_2) \end{array} \right] \)
\( = \left[ \begin{array}{ccc} 3/4 & 1/8 & 1/8 \\ 1/8 & 1/8 & 3/4 \end{array} \right] \)
とする。
このとき、次のエントロピーを求めなさい。
ただし、
\( \log_2 3 = 1.58 \)、\( \log_2 5 = 2.32 \)、\( \log_2 7 = 2.81 \)、\( \log_2 11 = 3.46 \)、
\( \log_2 13 = 3.70 \)、\( \log_2 17 = 4.09 \)、\( \log_2 19 = 4.25 \)
として小数点以下2桁の小数で解答しなさい。
(1) \(X\) のエントロピー \(H(X)\) (単位は [bit/記号] として数値のみ解答すること)
(2) \(Y\) のエントロピー \(H(Y)\) (単位は [bit/記号] として数値のみ解答すること)
(3) 結合エントロピー \(H(X,Y)\) (単位は [bit/記号] として数値のみ解答すること)
(4) 相互エントロピー \(I(X;Y)\) (単位は [bit/記号] として数値のみ解答すること)
2020年 6月 1日
問1. 誤りのない \( 2^m \) 元通信路の通信路容量を示し、なぜそのようになるかを説明しなさい。
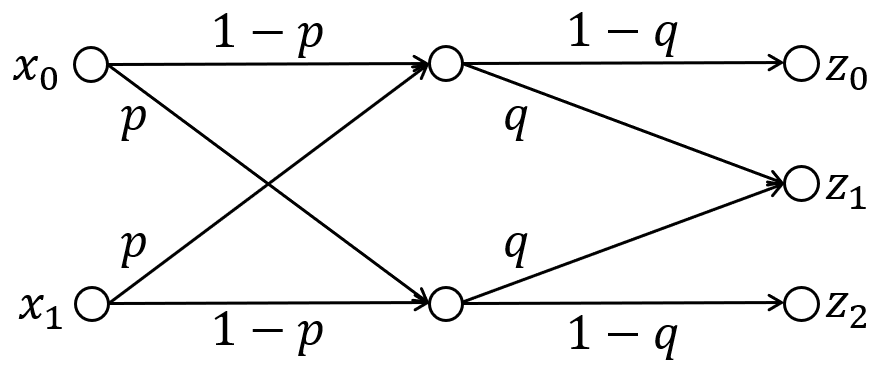
問2. 下図に示す通信路の通信路容量を求め、その通信路容量を求める過程を説明しなさい。
