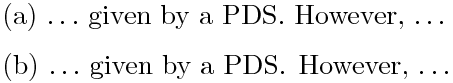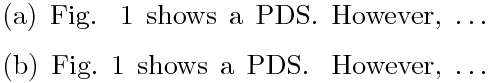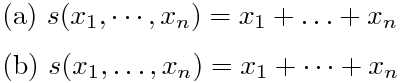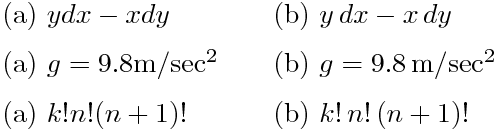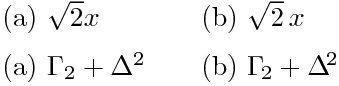Tips/TeX/Аµ¤·¤¤ҐЮЎјҐЇҐўҐГҐЧ
ЎЦTeX¤т»И¤Ё¤РЎўїфј°¤ОВї¤¤КёЅс¤тИуѕп¤ЛИю¤·¤ЇБИИЗ¤№¤л¤і¤И¤¬¤З¤¤Ю¤№ЎЈЎЧЎДіО¤«¤Л¤Ѕ¤¦¤К¤О¤З¤№¤¬Ўў¤і¤ОКё¤Л¤ПЎЦГшјФ¤¬TeX¤тНэІт¤·¤Ж»И¤¤¤і¤К¤»¤РЎЧ¤И¤¤¤¦Гў¤·Ѕс¤¤¬Й¬НЧ¤З¤ў¤л¤и¤¦¤Л»Ч¤¤¤Ю¤№*1ЎЈ
TeX¤ПЎўЙФЙ¬НЧ¤ЛГшјФ¤О°ХїЮ¤тїдВ¬¤·¤и¤¦¤И¤П¤·¤Ю¤»¤уЎЈ¤Ѕ¤О¤ї¤бЎў¤И¤¤Л¤ПЎў»ж¤Л±фЙ®¤ЗЅс¤Ї¤И¤¤ИЖ±¤ёЅс¤Кэ¤З¤ПЙФЅЅК¬¤ЗЎўј«К¬¤О°ХїЮ¤тАµ¤·¤ЇTeX¤ЛЕБ¤Ё¤л¤и¤¦¤ЛГн°Хїј¤ЇµЅТ¤·¤К¤±¤м¤Р¤¤¤±¤К¤¤¤і¤И¤в¤ў¤к¤Ю¤№ЎЈ
°КІј¤З¤ПЎў¤и¤Їё«¤«¤±¤лЎЦАµ¤·¤Ї¤К¤¤ҐЮЎјҐЇҐўҐГҐЧЎЧ¤ООг¤И¤Ѕ¤ОЅ¤Аµ°Ж¤тѕТІр¤·¤Ю¤№ЎЈ
ЛЬКёГж¤Оµ№ж†
ҐФҐкҐЄҐЙ†
TeX¤ПЎў±СёмКё¤ОКёЛц¤ЛЎўДМѕп¤ОГ±ёмґЦ¤и¤к№¤¤¶хЗт¤тГЦ¤¤Ю¤№ЎЈКёЛц¤ПЅЄ»ЯЙдЎК¤Ю¤ї¤ПµїМдЙд¤Ю¤ї¤Пґ¶ГІЙдЎЛ¤Л¤и¤Г¤ЖЙЅ¤µ¤м¤Ю¤№¤¬ЎўҐФҐкҐЄҐЙ(.)¤ПЅЄ»ЯЙд¤И¤·¤Ж°Кі°¤ЛЎўFig.¤К¤Й¤ОѕКО¬µЛЎ¤З¤в»И¤п¤м¤Ю¤№ЎЈ¤і¤м¤ЛВР¤№¤лTeX¤ОЅиНэµ¬В§¤ПГ±Ѕг¤ЗЎўЎЦ(1)ВзКё»ъ¤Оёе¤н¤ОҐФҐкҐЄҐЙ¤ПЅЄ»ЯЙд¤З¤П¤К¤¤ЎЈ(2)¤Ѕ¤м°Кі°¤ОҐФҐкҐЄҐЙ¤ПЅЄ»ЯЙд¤З¤ў¤лЎЈЎЧ¤И¤К¤к¤Ю¤№ЎЈ¤і¤Оµ¬В§¤Л№з¤п¤К¤¤ѕм№з¤ПЎўҐЮЎјҐЇҐўҐГҐЧ¤тК䤦ɬНЧ¤¬¤ў¤к¤Ю¤№ЎЈ
(a) $\ldots$ given by a PDS. However, $\ldots$ (b) $\ldots$ given by a PDS\@. However, $\ldots$
ВзКё»ъ¤ЗЅЄ¤п¤лКё¤тЅс¤Ї¤И¤¤ПЎўєЗёе¤ОВзКё»ъ¤ИҐФҐкҐЄҐЙ¤ОґЦ¤ЛКМ¤ОІї¤«¤т¶ґ¤у¤ЗЎўѕеµ¤Оµ¬В§(1)¤¬Е¬НС¤µ¤м¤К¤¤¤и¤¦¤Л¤·¤Ю¤№ЎЈОг¤Ё¤РОг(b)¤О¤и¤¦¤Л \@ ¤т¶ґ¤Я¤Ю¤№ЎЈ¤ў¤Ю¤кБИИЗ·лІМ¤Лє№¤¬¤К¤¤¤и¤¦¤З¤№¤¬Ўў°КІј¤О¤и¤¦¤ЛЎЦ¤ж¤л¤ЇЎЧБИИЗ¤µ¤м¤їѕм№зЎК№ФЙэ¤Л№з¤п¤»¤л¤ї¤б¤Л¶хЗт¤тї¤Р¤·¤їѕм№зЎЛ¤Л¤Пє№¤¬¤и¤ЇМЬО©¤Б¤Ю¤№ЎЈ
¤К¤ЄЎўКД¤ёізёМ¤ПКёЛц¤«¤Й¤¦¤«¤ОИЅГЗ¤ОєЭ¤ЛМµ»л¤µ¤м¤л¤О¤ЗЎўЎЦ... pushdown system (PDS).ЎЧ¤О¤и¤¦¤КізёМ¤ЗЅЄ¤п¤лКё¤вЎў... pushdown system (PDS)\@. ¤О¤и¤¦¤ЛЅс¤ЇЙ¬НЧ¤¬¤ў¤к¤Ю¤№ЎЈїфј°¤ПЎЦВзКё»ъ¤З¤П¤К¤¤ЎЧ¤И°·¤п¤м¤Ю¤№¤О¤ЗЎўїфј°¤ЗЅЄ¤п¤лКёЎКОг¤Ё¤РЎЦ... denoted by~$S$.ЎЧЎЛ¤Л¤П \@ ¤тК䤦ɬНЧ¤П¤ў¤к¤Ю¤»¤уЎЈ
(a) $\ldots$ shown in Fig. 1. (b) $\ldots$ shown in Fig.~1.
µХ¤ЛЎўѕКО¬µЛЎ¤т»И¤¦¤И¤¤Л¤П¤·¤Р¤·¤РЎўҐФҐкҐЄҐЙ¤¬ЅЄ»ЯЙд¤З¤К¤¤¤і¤И¤тјЁ¤№Й¬НЧ¤¬Аё¤ё¤Ю¤№ЎЈОг(a)¤З¤П Fig. ¤И1¤ОґЦ¤¬і«¤Іб¤®¤Ж¤¤¤Ю¤№ЎЈ¤і¤м¤вЎЦ¤ж¤л¤ЇЎЧБИИЗ¤µ¤м¤ї¤И¤¤Л¤ПЎў°КІј¤О¤и¤¦¤Лє№¤¬¤П¤Г¤¤к¤·¤Ю¤№ЎЈ
Dr.Ўўet al.Ўўresp.Ўў¤К¤Й¤ОѕКО¬µЛЎ¤вЖ±НН¤З¤№*2ЎЈ
¤і¤м¤й¤Оѕм№з¤ПЎўҐФҐкҐЄҐЙ¤Оёе¤н¤ЛМАјЁЕЄ¤ЛЎЦГ±ёмґЦ¤О¶хЗтЎЧ¤тГЦ¤±¤Р¤и¤ЇЎў¤ї¤¤¤Ж¤¤¤ПОг(b)¤О¤и¤¦¤ЛЎЦ№ФК¬ід¤µ¤м¤К¤¤¶хЗтЎЧ¤тЙЅ¤№ҐЖҐЈҐлҐА(~)¤т»И¤Ё¤Р¤и¤¤¤З¤№ЎЈFig.\ 1 ¤О¤и¤¦¤Л \ ЙХ¤¤О¶хЗт¤тГЦ¤ЇКэЛЎ¤в¤ў¤к¤Ю¤№¤¬ЎўFig. ¤И 1 ¤П¤Т¤И¤Ю¤И¤Ю¤к¤И№Н¤Ё¤ЖЎўЎЦ№ФК¬ід¤µ¤м¤К¤¤¶хЗтЎЧ¤т»И¤Г¤ї¤Ы¤¦¤¬¤и¤¤¤З¤·¤з¤¦ЎЈКёёҐҐкҐ№ҐИГж¤З¤ОѕКО¬·Б¤К¤Й¤З¤ПЎўTrans.\ Inf.\ \& Syst. ¤О¤и¤¦¤Л \ ЙХ¤¶хЗт¤¬¤и¤¤¤З¤·¤з¤¦ЎЈ
ҐПҐ¤ҐХҐуЎўҐАҐГҐ·ҐеЎўҐЮҐ¤ҐКҐ№†
(a) -2, -1, 0, 1 (b) $-2$, $-1$, $0$, $1$
Ог(a)¤З¤П Ўј ¤¬ҐЮҐ¤ҐКҐ№µ№ж¤З¤П¤К¤ЇҐПҐ¤ҐХҐу¤И¤·¤ЖБИИЗ¤µ¤м¤Ж¤¤¤Ю¤№ЎЈ(b)¤О¤и¤¦¤Лїфј°¤Л¤№¤лЎК$¤З°П¤аЎЛ¤О¤¬Е¬АЪ¤З¤№ЎЈ¤К¤ЄЎўЙд№ж¤О¤К¤¤0¤д1¤Пїфј°¤Л¤·¤К¤Ї¤Ж¤в№Ѕ¤п¤К¤¤¤И»Ч¤¤¤Ю¤№¤¬ЎўЛЬКё¤ОҐХҐ©ҐуҐИ¤Иїфј°НСҐнЎјҐЮҐуҐХҐ©ҐуҐИ¤¬°Ы¤К¤лѕм№зЎКtimesҐСҐГҐ±ЎјҐё¤т»И¤Г¤Ж¤¤¤л¤И¤¤К¤ЙЎЛ¤ПЎў$¤З°П¤у¤Аїф»ъ¤И¤Ѕ¤¦¤З¤К¤¤їф»ъ¤И¤З»ъВО¤¬КС¤п¤л¤і¤И¤Л¤К¤к¤Ю¤№ЎЈ
(a) pp.1-3 (b) pp.1--3
ИП°П¤тЙЅ¤№¤Л¤ПЎў(a)¤ОҐПҐ¤ҐХҐу¤и¤к(b)¤ОЖуК¬ҐАҐГҐ·Ґе¤¬Е¬АЪ¤З¤№*3ЎЈ
їфј°†
Г±ём†
(a) $difference=x-y$
(b) $\mathit{difference}=x-y$
їфј°НСҐ¤ҐїҐкҐГҐЇҐХҐ©ҐуҐИ¤ПЎў1»ъ1»ъ¤¬¤Ѕ¤м¤ѕ¤мКСїф¤З¤ў¤л¤и¤¦¤К»И¤¤Кэ¤тБЫДк¤·¤ЖҐЗҐ¶Ґ¤Ґу¤µ¤м¤Ж¤¤¤Ю¤№¤О¤ЗЎўКЈїфКё»ъ¤«¤й¤К¤лГ±ём¤тЙЅ¤№¤О¤Л¤Пёю¤¤¤Ж¤¤¤Ю¤»¤уЎЈdifference¤ПЖГ¤ЛЙФєЩ№©¤КОг¤З¤№¤¬Ўў¤Ы¤«¤ОГ±ём¤З¤вЎў¤Й¤і¤«¤·¤йКё»ъґЦіЦ¤¬ЙФј«Бі¤Кґ¶¤ё¤Л¤К¤л¤і¤И¤¬Вї¤¤¤З¤№ЎЈ\mathit¤д\mathrm¤К¤Й¤т»И¤¦¤О¤¬Е¬АЪ¤З¤№ЎЈ
±й»»»Т†
TeX¤ПЎўїфј°НСµ№ж¤тЎЦЖу№а±й»»»ТЎЧЎЦґШ·ё±й»»»ТЎЧ¤К¤Й¤ЛК¬Оа¤·¤ЖЎў¤Ѕ¤м¤Лґр¤Е¤¤¤Жµ№жґЦ¤ОґЦіЦ¤тДґАб¤·¤Ж¤¤¤Ю¤№ЎЈTeX¤Л¤и¤лК¬Оа¤И°Ы¤К¤л»И¤¤Кэ¤т¤№¤лѕм№з¤Л¤ПЎў¤Ѕ¤О¤і¤И¤тҐЮЎјҐЇҐўҐГҐЧ¤Л¤и¤Г¤ЖјЁ¤№Й¬НЧ¤¬¤ў¤к¤Ю¤№ЎЈ
(a) $ \to \subseteq Q\times Q$
(b) ${\to}\subseteq Q\times Q$
Ог(a)¤З¤П ўЄ ¤И ўј ¤¬¤Ї¤Г¤Д¤¤¤Ж¤·¤Ю¤Г¤Ж¤¤¤Ю¤№ЎЈ¤і¤м¤ПОѕјФ¤¬ґШ·ё±й»»»Т¤З¤ў¤л¤ї¤б¤З¤№ЎЈґШ·ё±й»»»Т¤¬КВ¤у¤З¤¤¤лѕм№з¤Л¤ПЎўTeX¤П¤Ѕ¤м¤й¤т¤Ї¤Г¤Д¤±¤ї¤в¤ОБґВО¤т°м¤Д¤ОґШ·ё±й»»»Т¤О¤и¤¦¤Л°·¤¤¤Ю¤№ЎКОг¤Ё¤Р := ¤К¤ЙЎЛЎЈµ№ж¤дЙфК¬ј°¤т { } ¤З°П¤а¤ИЎў°П¤Ю¤м¤їЙфК¬¤¬ЎЦЙбДМ¤Оµ№жЎЧ°·¤¤ЎКїф»ъ¤д±С»ъ¤ИЖ±¤ёЎЛ¤Л¤К¤к¤Ю¤№ЎЈ
(a) $D\uparrow =\{d_1,d_2,\ldots,d_k\}$
(b) $D{\uparrow}=\{d_1,d_2,\ldots,d_k\}$
\uparrow ¤ПґШ·ё±й»»»Т¤К¤О¤ЗЎўЖ±¤ё¤ЇґШ·ё±й»»»Т¤З¤ў¤л = ¤И¤Ї¤Г¤Д¤¤¤Ж¤·¤Ю¤¤¤Ю¤№ЎЈ¤Д¤Ю¤кОг(a)¤ПTeX¤«¤йё«¤л¤ИЎЦD ¤И { d1,... } ¤т ў¬= ¤З·л¤у¤Ај°ЎЧ¤Л¤К¤к¤Ю¤№ЎЈЎЦD¤Л±й»»ў¬¤тЕ¬НС¤·¤ї·лІМ¤¬ { d1,... } ¤ЛЕщ¤·¤¤ЎЧ¤ИЅс¤¤ї¤¤¤К¤йЎў\uparrow ¤тЎЦЙбДМ¤Оµ№жЎЧ¤Л¤№¤лЙ¬НЧ¤¬¤ў¤к¤Ю¤№ЎЈ
(a) $a=1\land b=2$ (b) $(a=1)\land(b=2)$
\land ¤ПЖу№а±й»»»Т¤К¤О¤ЗЎў+ ¤К¤Й¤ИЖ±¤ё°·¤¤¤З¤№ЎЈ¤З¤№¤О¤ЗЎўОг¤Ё¤РЎЦa=1+b=2ЎЧ¤И¤¤¤¦ј°¤¬ЎЦa ¤И 1+b ¤И 2 ¤тЕщ№ж¤З·л¤у¤Ај°ЎЧ¤ИІтјб¤µ¤м¤л¤О¤ИЖ±НН¤ЛЎўОг(a)¤ПЎЦa ¤И 1ўКb ¤И 2 ¤тЕщ№ж¤З·л¤у¤Ај°ЎЧ¤ИІтјб¤µ¤м¤Ю¤№ЎЈ¤і¤Оѕм№з¤ПізёМ¤тКд¤Г¤ЖЫЈЛ椵¤т¤К¤Ї¤№¤О¤¬Е¬АЪ¤И»Ч¤¤¤Ю¤№ЎЈ
ҐіҐуҐЮ†
(a) $a=1, b=2$ (b) $a=1,\ b=2$
їфј°Гж¤З¤ОҐіҐуҐЮ(,)¤ПЎўf(x,y) ¤О¤и¤¦¤К°ъїфҐкҐ№ҐИ¤дҐЩҐЇҐИҐл¤ОА®К¬¤ОҐкҐ№ҐИ¤Л»И¤¦¤і¤И¤¬БЫДꤵ¤м¤Ж¤¤¤л¤ї¤бЎўҐіҐуҐЮ¤Оёе¤н¤Л¤ў¤Ю¤к¶хЗт¤¬і«¤¤Ю¤»¤уЎЈ¤Ѕ¤О¤ї¤бЎўОг(a)¤ПЎЦa ¤И 1,b ¤И 2 ¤тЕщ№ж¤З·л¤у¤Ај°ЎЧ¤О¤и¤¦¤Лё«¤Ё¤Ж¤·¤Ю¤¤¤Ю¤№ЎК¤К¤ЄЎўїфј°Гж¤З¤П¶хЗтКё»ъ¤ПМµ»л¤µ¤м¤Ю¤№ЎЛЎЈ(b)¤О¤и¤¦¤ЛЎў\ ЙХ¤¤ОМАјЁЕЄ¤К¶хЗт¤тГЦ¤±¤РЎў¤ў¤лДшЕЩ¤ОЙэ¤О¶хЗт¤¬ГЦ¤«¤м¤Ю¤№ЎЈ¤в¤Г¤И№¤¤¶хЗтЎК\quad¤д\qquadЎЛ¤¬Е¬АЪ¤Кѕм№з¤в¤ў¤л¤·Ўўїфј°¤¬К¤Фʤ¤¤и¤¦¤ЛГ±ём¤т¶ґ¤у¤А¤Ы¤¦¤¬¤и¤¤ѕм№з¤в¤ў¤к¤Ю¤№ЎЈ
(a) $a=1,234,567$
(b) $a=1{,}234{,}567$
(b') $a={}$1,234,567
µХ¤ЛЎў°Мји¤к¤О¤ї¤б¤ОҐіҐуҐЮ¤Оѕм№з¤ПЎў¤Ѕ¤Оёе¤н¤Л¶хЗт¤тГЦ¤«¤К¤¤¤Ы¤¦¤¬Е¬АЪ¤З¤№ЎЈ¤і¤О¤И¤¤ПОг(b)¤О¤и¤¦¤ЛЎўҐіҐуҐЮ¤т { } ¤З°П¤у¤ЗЙбДМ¤Оµ№ж¤Л¤·¤Ю¤№ЎЈОг(b')¤О¤и¤¦¤Лїф»ъ¤тїфј°¤Оі°¤ЛЅР¤№КэЛЎ¤в¤ў¤к¤Ю¤№ЎЈОг(b')¤З¤ПЎў= ¤Иїф»ъ¤ОґЦ¤ЛЕ¬АЪ¤КЙэ¤О¶хЗт¤¬Жю¤л¤и¤¦Ўў¶х¤Оїфј° {} ¤тБЮЖю¤·¤Ж¤¤¤Ю¤№ЎЈ
ѕКО¬µ№ж†
(a) $s(x_1,\cdots,x_n)=x_1+\ldots+x_n$ (b) $s(x_1,\ldots,x_n)=x_1+\cdots+x_n$
Ог(a)¤ПІї¤А¤«¤Б¤°¤П¤°¤ЗЙФіК№Ґ¤З¤№¤НЎЈҐіҐуҐЮ¤ИҐіҐуҐЮ¤ОґЦ¤П \ldots ¤т»И¤¤¤Ю¤№ЎЈ+ЎўЎјЎўЎЯЎў=Ўўўѕ ¤К¤ЙЎўѕеІјВРѕО¤Оµ№ж¤ОґЦ¤Л¤П \cdots ¤¬Е¬АЪ¤З¤№ЎЈ¤Й¤Б¤й¤«МВ¤¦ѕм№з¤П \ldots ¤Л¤·¤Ж¤Є¤±¤РМµЖс¤З¤№ЎЈ
¶иАЪ¤кµ№ж†
(a) $x=<a,b>$ (b) $x=\langle a,b\rangle$ (b') $x=\left<a,b\right>$
»і·їізёМ¤т»И¤¤¤ї¤¤¤И¤¤ПЎўЙФЕщ№жЎК< >ЎЛ¤З¤П¤К¤Ї \langle \rangle ¤т»И¤¤¤Ю¤№ЎЈ(a)¤О¤и¤¦¤ЛізёМ¤ОВе¤п¤к¤ЛЙФЕщ№ж¤т»И¤¦¤И¤ї¤¤¤Ш¤уЙФєЩ№©¤З¤№ЎЈ(b')¤О¤и¤¦¤Л \left< \right> ¤т»И¤Г¤Ж¤в¤и¤¤¤З¤№ЎЈ\left \right ¤т»И¤Г¤їѕм№з¤ПЎў¶ґ¤Ю¤м¤лЙфК¬ј°¤О№в¤µЎ¦їј¤µ¤Л№з¤п¤»¤ЖізёМ¤ОВ礤µ¤¬КСІЅ¤·¤Ю¤№ЎЈ\left\langle \right\rangle ¤ИЅс¤¤¤Ж¤в(b')¤ИЖ±¤ё¤Л¤К¤к¤Ю¤№ЎЈ
(a) $\{x| ||x||>0\}$
(b) $\{\,x\mid \|x\|>0\,\}$
ЅДАю(|)¤ПАдВРГНЎКОг¤Ё¤Р |x|ЎЛ¤К¤Й¤тЙЅ¤№µ№ж¤З¤№ЎЈ¤і¤ООг¤О¤и¤¦¤КЎўЅё№з¤ОДкµБГж¤О¶иАЪ¤кАю¤ПЎўґШ·ё±й»»»Т¤З¤ў¤л \mid ¤т»И¤Г¤ЖЅс¤¤Ю¤№ЎЈ¤Ю¤їЎўЖуЅЕЅДАю¤тЅс¤¤ї¤¤¤И¤¤ПЎў|| ¤З¤П¤К¤Ї \| ¤т»И¤¤¤Ю¤№ЎЈ|| ¤З¤ПЅДАюґЦ¤ОґЦіЦ¤¬№¤№¤®¤ЖЎўґЦ±д¤У¤·¤Ж¤·¤Ю¤¤¤Ю¤№ЎЈ\, ¤ПєЩ¤¤¶хЗт¤тГЦ¤ЇМїОб¤З¤№ЎЈЅДАю¤т»И¤Г¤їЅё№з¤ОДкµБЎКЖвКсЕЄДкµБЎЛ¤тЅс¤Ї¤И¤¤ПЎўГжізёМ¤ОЖвВ¦¤ЛєЩ¤¤¶хЗт¤тГЦ¤Ї¤О¤¬¤и¤¤¤Ѕ¤¦¤З¤№ЎКTeXbook [K89, p.239] ¤и¤кЎЛЎЈ
(a) $|-x|=|+x|$ (b) $\left|-x\right|=\left|+x\right|$
[K89, p.235] ¤ЛєЬ¤Г¤Ж¤¤¤лОгЎЈГ±¤ЛЅДАю¤тЅс¤¤¤їѕм№зЎў¤Ѕ¤м¤ПЎЦЙбДМ¤Оµ№жЎЧ¤И¤·¤Ж°·¤п¤м¤Ю¤№ЎЈ¤Ѕ¤О¤ї¤бЎўОг(a)¤З¤ПЎўTeX¤ПЎЦ | ¤«¤й x| ¤тёє¤ё¤ї¤в¤О¤И | ¤Л x| ¤тІГ¤Ё¤ї¤в¤О¤¬Ещ¤·¤¤ЎЧ¤ИІтјб¤·ЎўНѕК¬¤К¶хЗт¤тБЮЖю¤·¤Ж¤·¤Ю¤¤¤Ю¤№ЎЈЙбДМ¤Оµ№ж¤З¤П¤К¤Ї¶иАЪ¤кµ№ж¤З¤ў¤л¤і¤И¤тјЁ¤№¤ї¤бЎў\left \right ¤т»И¤¦Й¬НЧ¤¬¤ў¤к¤Ю¤№ЎЈ
¶хЗт†
(a) $y dx-x dy$
(b) $y\,dx-x\,dy$
(a) $g=9.8{\rm m/sec^2}$
(b) $g=9.8\,{\rm m/sec^2}$
(a) $k!n!(n+1)!$
(b) $k!\,n!\,(n+1)!$
¤¤¤є¤м¤в [K89, p.232] ¤и¤кЎЈєЩ¤¤¶хЗт(\,)¤тК䤦¤О¤¬Лѕ¤Ю¤·¤¤Ог¤З¤№ЎЈdx ¤д dy ¤ОБ°ЎўКЄНэГ±°М¤ОБ°Ўўі¬ѕиµ№ж( ! )¤И±Сїф»ъ¤ді«¤ізёМ¤ОґЦЎў¤Л¤ПєЩ¤¤¶хЗт¤тГЦ¤Ї¤О¤¬¤и¤¤¤ИЅТ¤Щ¤й¤м¤Ж¤¤¤Ю¤№ЎЈ
(a) $\sqrt2 x$
(b) $\sqrt2\,x$
(a) $\Gamma_2+\Delta^2$
(b) $\Gamma_{\!2}+\Delta^{\!2}$
[K89, p.233] ¤и¤кЎЈєЩ¤¤¶хЗт¤тГЦ¤Ї¤О¤¬Лѕ¤Ю¤·¤¤ОгЎў¤Є¤и¤УЎўµХ¤ЛЙй¤О¶хЗт(\!)¤тГЦ¤¤¤ЖґЦіЦ¤тµН¤б¤ї¤Ы¤¦¤¬¤и¤¤ОгЎў¤З¤№ЎЈ¤і¤м¤й¤ПЎў°мЕЩБИИЗ¤т¤·¤Ж¤Я¤ЖЎўЙФєЩ№©¤Лґ¶¤ё¤ї¤йЅ¤Аµ¤№¤лЎў¤И¤¤¤¦КэїЛ¤ЗА°¤Ё¤л¤О¤¬¤и¤¤¤З¤·¤з¤¦ЎЈ
»І№НКёёҐ†
[K89] D.E. Knuth, TeXҐЦҐГҐЇ, ІюДыї·ИЗ, єШЖЈї®ГЛґЖЅ¤, єнГ«№Ґµ±Мх, ҐўҐ№ҐЎј, 1989.
*1 TeX¤ОґрЛЬҐіҐуҐ»ҐЧҐИ¤ПЎЦKnuthАиАё¤¬ј«Гш¤т»Ч¤¤ДМ¤к¤ЛҐЗҐ¶Ґ¤Ґу¤№¤л¤ї¤б¤ОҐДЎјҐлЎЧ¤З¤ў¤кЎў·и¤·¤ЖЎЦГЇ¤З¤вґКГ±¤ЛИю¤·¤¤БИИЗ·лІМ¤¬ЖА¤й¤м¤лЎЧ¤З¤П¤К¤¤¤О¤З¤№ЎДЎЈ
*2 TeX¤И¤ПґШ·ё¤К¤¤¤З¤№¤¬Ўўet al. ¤О et ¤П¤і¤м¤З1Г±ёмЎК±Сём¤Оand¤ЛЕц¤ї¤лЎЛ¤К¤О¤ЗЎўёе¤н¤ЛҐФҐкҐЄҐЙ¤тЙХ¤±¤Ю¤»¤уЎЈ
*3 ¤і¤м¤вTeX¤И¤ПґШ·ё¤К¤¤¤З¤№¤¬Ўўp. = page (Г±їф·Б)Ўўpp. = pages (КЈїф·Б) ¤З¤№ЎЈ
ЕєЙХҐХҐЎҐ¤Ґл: