


: 付録
ディジタル信号処理論 演習問題 12
学籍番号
氏名
- 法を 5とした場合の
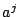 の剰余(
の剰余(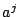 (mod 5))の値を
(mod 5))の値を 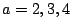 、
、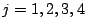 について求めなさい。
について求めなさい。
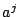 |
1 |
2 |
3 |
4 |
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
- GF(2)上の多項式
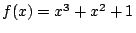 は、
は、
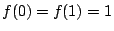 であることから、GF(2)に
であることから、GF(2)に 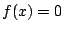 の解(零点)を持たない。
すなわち、
の解(零点)を持たない。
すなわち、
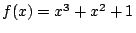 は GF(2)上既約である。
は GF(2)上既約である。
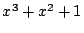 の解を
の解を 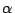 とすると、GF(2) の拡大体が
とすると、GF(2) の拡大体が
によって定義できることを示しなさい。
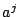 (mod 5)
(mod 5)
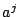 |
1 |
2 |
3 |
4 |
| 2 |
2 |
4 |
3 |
1 |
| 3 |
3 |
4 |
2 |
1 |
| 4 |
4 |
1 |
4 |
1 |
フェルマーの小定理(付録参照)
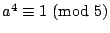 が成立していることがわかる。
が成立していることがわかる。
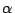 は
は
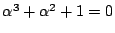 を満たす。
したがって
を満たす。
したがって
である。
この関係を使って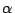 のべきを順に求めると
のべきを順に求めると
となるから、2次以下の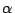 の多項式すべてが0と
の多項式すべてが0と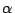 のべきで表現できる。
したがって、
のべきで表現できる。
したがって、
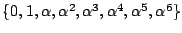 は位数 8の体をなす。
は位数 8の体をなす。



: 付録
FUKUMOTO Masahiro
平成17年7月25日
![]() の解を
の解を ![]() とすると、GF(2) の拡大体が
とすると、GF(2) の拡大体が
![]() の解を
の解を ![]() とすると、GF(2) の拡大体が
とすると、GF(2) の拡大体が