情報理論基礎 試験問題（2011年度）

2011年 6月 2日

問 1. $M$元記号 $S=\left\{ s_1, s_2, \cdots, s_M \right\}$ で表現できる情報量の定義とその最大値を示しなさい。

問 2. 送信記号を {“0”,“1”} とするような2元通信系で、 送信記号 “0” に対する受信信号が、期待値 $\mu=-0.2$、分散 $\sigma^2=1/25$ の正規分布に従うとする。 この通信系で “0” を送信したときに判定を誤る確率（記号誤り率）を 0.01 以下にするための判定しきい値（受信信号がしきい値以下であれば “0” と判定する）を求めなさい。

問 3. 新規に計画している通信システムでは、記号 $a$、$b$、$c$、$s$ を送信すると、 それぞれ 0.006、0.001、0.002、0.001 の確率で受信時の記号誤りが発生する。 また、この記号 $a$、$b$、$c$、$d$ は、それぞれ 0.01、0.35、0.25、0.30 の確率で送信されることがわかっている。 このとき、次の問いに答えなさい。

(1) この通信システムで正しく受信できる確率を求めなさい。

(2) この通新システムで記号誤りが起こったときに、送信された信号が $b$ によるものである確率を求めなさい。

問 4. 情報源 $S = \left\{ s_1, s_2, s_3, s_4, s_5 \right\}$ を次の $C_1 \sim C_4$のように2元符号化した。

	$C_1$	$C_2$	$C_3$	$C_4$
$s_1$	000	1100	0	1110
$s_2$	001	111	10	110
$s_3$	010	0	111	0
$s_4$	011	1101	1100	11110
$s_5$	100	10	1101	10

　情報源$S$の生起確率を

$$S = \left\{ \begin{array}{ccccc} s_1, & s_2, & s_3, & s_4, & s_5 \\ 1/24, & 5/24, & 5/12, & 1/12, & 1/4 \end{array} \right\}$$

として、符号 $C_1 \sim C_4$について以下の問に答えなさい。

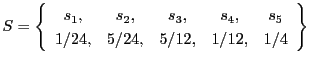
(1) 符号の木を用いて、 $C_1 \sim C_4$のうち瞬時符号であるものをすべてあげなさい。

(2) (1)で求めた瞬時符号すべての効率を求め、最も効率の良いものを示しなさい。

　ただし、 $\log_2 3 = 1.58$、 $\log_2 5 = 2.32$、 $\log_2 7 = 2.81$、 $\log_2 11 = 3.46$として計算しなさい。

問 5. 通信路行列が

$$P = \left[ \begin{array}{cc} \displaystyle\frac{15}{16} & \di... ... \displaystyle\frac{1}{16} & \displaystyle\frac{15}{16} \end{array} \right]$$

である通信路の通信路容量を求めなさい。 ただし、 $\log_2 3 = 1.58$、 $\log_2 5 = 2.32$、 $\log_2 7 = 2.81$、 $\log_2 11 = 3.46$として計算しなさい。