ディジタル信号処理論 演習問題 6

情報システム工学コース

2005年 6月27日

学籍番号 氏名

1. 整数の集合$Z$の任意の元$x, y$を正整数$m$で割った余りが等しいとき、``$x$と$y$は$m$を法として合同である'' といい、 $x \equiv y \ (\mbox{mod } m)$ と書く。

   　合同関係は同値関係である。 いま、$m=4$として以下の問に答えなさい。

   (1)

   上記合同関係による同値類を示しなさい。
   

   (2)

   同値類の間の2項関係として、加法、乗法を考え、その演算表を示しなさい。
   

   (3)

   剰余環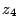$z_4$が零因子を持つことを示しなさい。

(1)

同値類はそれぞれ

$$\{ \cdots, -8, -4, 0, 4, 8, \cdots \}$$

$$\{ \cdots, -7, -3, 1, 5, 9, \cdots \}$$

$$\{ \cdots, -6, -2, 2, 6, 10, \cdots \}$$

$$\{ \cdots, -5, -1, 3, 7, 11, \cdots \}$$

となる。

(2)

加法、乗法の演算をそれぞれ $+$、$\times$で表すと、加算表と乗算表はそれぞれ下のようになる。

$+$	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

$\times$	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	0	2
3	0	3	2	1

(3)

$z_4 = \{ 0, 1, 2, 3 \}$ とすると、代数系 $(z_4, +, \times )$は環を成し、剰余環という。 その零元は 0 である。 $2 \ne 0$ に対して、$\times$の演算表より

$$2 \times 2 = 0$$

となる。 よって、2 はこの剰余環の零因子である。